Quadratic equation - Cuts
M(B) * M(D) =
M(A)^2 * z^(nb/2 + 2) * y^(wb) * x^(hb) + M(C)^2
I'll prove the equation
above with a bijection.
First consider the M(C)^2 term. We can represent that term by the
matching polynomial of the following graph, since the snake C is symmetrical:

If one of the pairs of z-edges connecting to B are not being used
in the matching then we can rearrange the parts of this graph to obtain
a matching of the graph D U B (D union B).
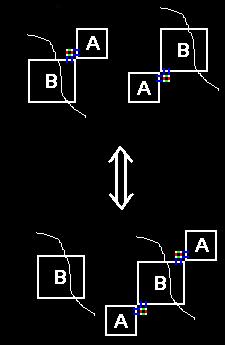
But if both pairs of z-edges are being used, then the B parts of
the graph have a common cut
. We can cut the graph and rearrange the parts to get a matching of
D U B:
Now, if we subtract
all the matchings above from the equation, here's what is left:
On the left hand side, we have all the matchings of D U B that do not
have a cut through the B part.
On the right hand side we have M(A)^2 * z^(nb/2 + 2) * y^(wb) * x^(hb)
But there is only one way to fill the B parts of D U B, such that there
is not cut through the B parts. So, we want to prove that:
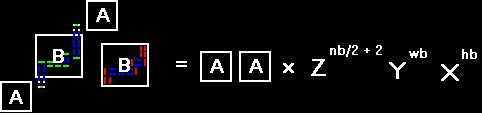
The A parts are disconnected in D and the matchings of the B parts multiplied
together gives us z^(nb/2 + 2) * y^(wb) * x^(hb).
QED